GPT-2 layer를 구현한 이후에, 실제 학습을 위한 optimizer 구현
You will further implement the step() function of the Adam Optimizer based on Decoupled Weight Decay Regularization and Adam: A Method for Stochastic Optimization in order to train a sentiment classifier.
Decoupled Weight Decay Regularization 및 Adam: A Method for Stochastic Optimization에 기반해서 AdamW optimizer를 직접 구현
Adam Optimzer
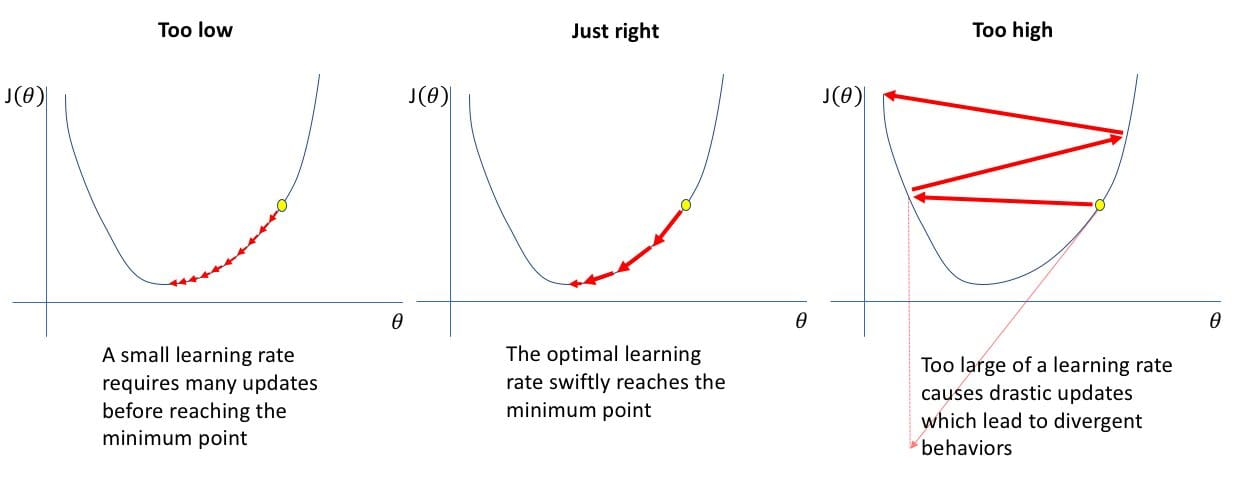
Adam은 SGD 기반의 옵티마이저로, 각각의 파라미터에 대해 1차 모멘트(mean)와 2차 모멘트(variance) 를 유지하면서 learning rate을 adapctive하게 조절해주는 방식 RMSProp과 Momentum의 장점을 모두 가져온 방식으로 널리 사용
SGD(Stochastic Gradient Descent) 전체 데이터 대신, 미니배치 또는 한 샘플을 기반으로 매번 파라미터를 업데이트 → 실제 학습할 corpus는 너무 많아서 언어모델에선 샘플링 방식으로 해결함
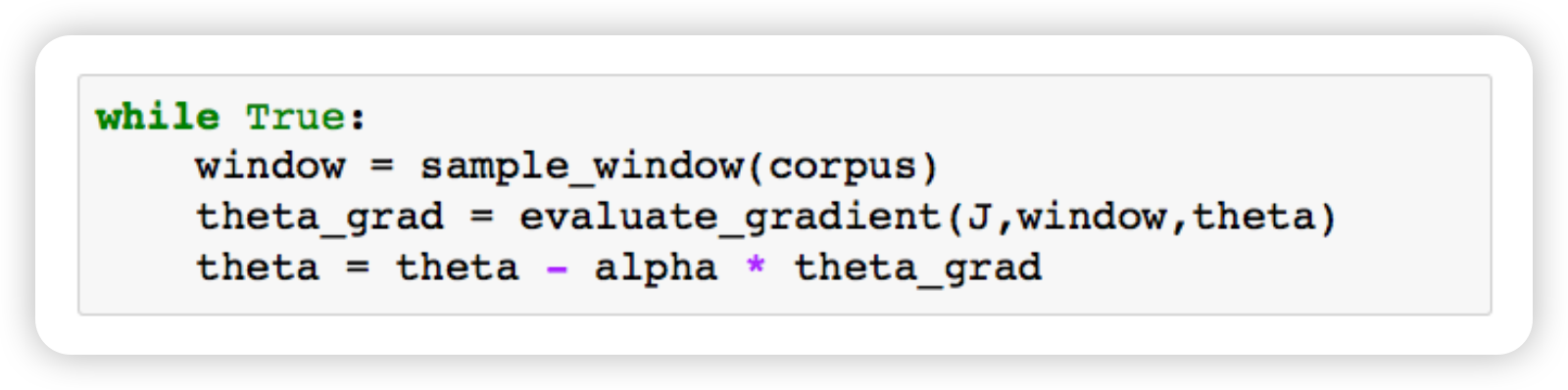
- 1차 모멘트: m_t ← gradient의 지수이동평균
- 2차 모멘트: v_t ← gradient 제곱의 지수이동평균
- 이 두 가지를 통해 parameter update 시 안정성 향상

기존 optimizer와 차이
AdamW는 기존 Adam과 달리 weight decay를 gradient에 포함시키지 않고, 파라미터 업데이트 이후 직접 decay시키는 구조
- Adam: grad ← grad + weight_decay * param 방식 → L2 Regularization처럼 작동
- AdamW: param ← param - lr * weight_decay * param 방식 → Decoupled 방식
⇒ weight decay를 옵티마이저 내부적으로 “분리해서 처리”함으로써 성능 안정성을 향상
구현
def step(self, closure: Callable = None):
loss = None
if closure is not None:
loss = closure()
for group in self.param_groups:
for p in group["params"]:
if p.grad is None:
continue
grad = p.grad.data
if grad.is_sparse:
raise RuntimeError("Adam does not support sparse gradients, please consider SparseAdam instead")
# State should be stored in this dictionary.
state = self.state[p]
# Access hyperparameters from the `group` dictionary.
alpha = group["lr"]
### TODO: Complete the implementation of AdamW here, reading and saving
### your state in the `state` dictionary above.
### The hyperparameters can be read from the `group` dictionary
### (they are lr, betas, eps, weight_decay, as saved in the constructor).
###
### To complete this implementation:
### 1. Update the first and second moments of the gradients.
### 2. Apply bias correction
### (using the "efficient version" given in https://arxiv.org/abs/1412.6980;
### also given in the pseudo-code in the project description).
### 3. Update parameters (p.data).
### 4. Apply weight decay after the main gradient-based updates.
###
### Refer to the default project handout for more details.
### YOUR CODE HERE
beta1, beta2 = group["betas"]
eps = group["eps"]
weight_decay = group["weight_decay"]
correct_bias = group["correct_bias"]
# 시작 단계 상태 초기화
if len(state) == 0:
state["step"] = 0
state["exp_avg"] = torch.zeros_like(p.data)
state["exp_avg_sq"] = torch.zeros_like(p.data)
exp_avg = state["exp_avg"] # m_t
exp_avg_sq = state["exp_avg_sq"] # v_t
state["step"] += 1
step = state["step"]
# 1차 모멘트
exp_avg.mul_(beta1).add_(grad, alpha=1 - beta1)
# 2차 모멘트
exp_avg_sq.mul_(beta2).addcmul_(grad, grad, value=1 - beta2)
# Bias correction
if correct_bias:
bias_correction1 = 1 - beta1 ** step
bias_correction2 = 1 - beta2 ** step
step_size = alpha * math.sqrt(bias_correction2) / bias_correction1
else:
step_size = alpha
denom = exp_avg_sq.sqrt().add_(eps)
# Parameter update
p.data.addcdiv_(exp_avg, denom, value=-step_size)
# Weight decay 를 gradient와 분리해서 적용
if weight_decay > 0.0:
p.data.add_(p.data, alpha=-alpha * weight_decay)
return loss
Our reference uses the “efficient” method of computing the bias correction mentioned at the end of section 2 “Algorithm” of in Kigma and (and at the end of the algorithm above) in place of the intermediate m_hat and v_hat method. Similarly, the learning rate should be incorporated into the weight decay update
위에 언급된 알고리즘과 다르게 “efficient method” 를 적용한 방법
기존 알고리즘
m̂_t = m_t / (1 - β1^t)
v̂_t = v_t / (1 - β2^t)
θ_t = θ_t - α * m̂_t / (sqrt(v̂_t) + ε)
efficient method
step_size = α * sqrt(1 - β2^t) / (1 - β1^t)
θ_t = θ_t - step_size * m_t / (sqrt(v_t) + ε)
m_t, v_t는 그대로 사용하고, 보정 계수를 step_size 계산 시 learning rate에 함께 곱해서 처리